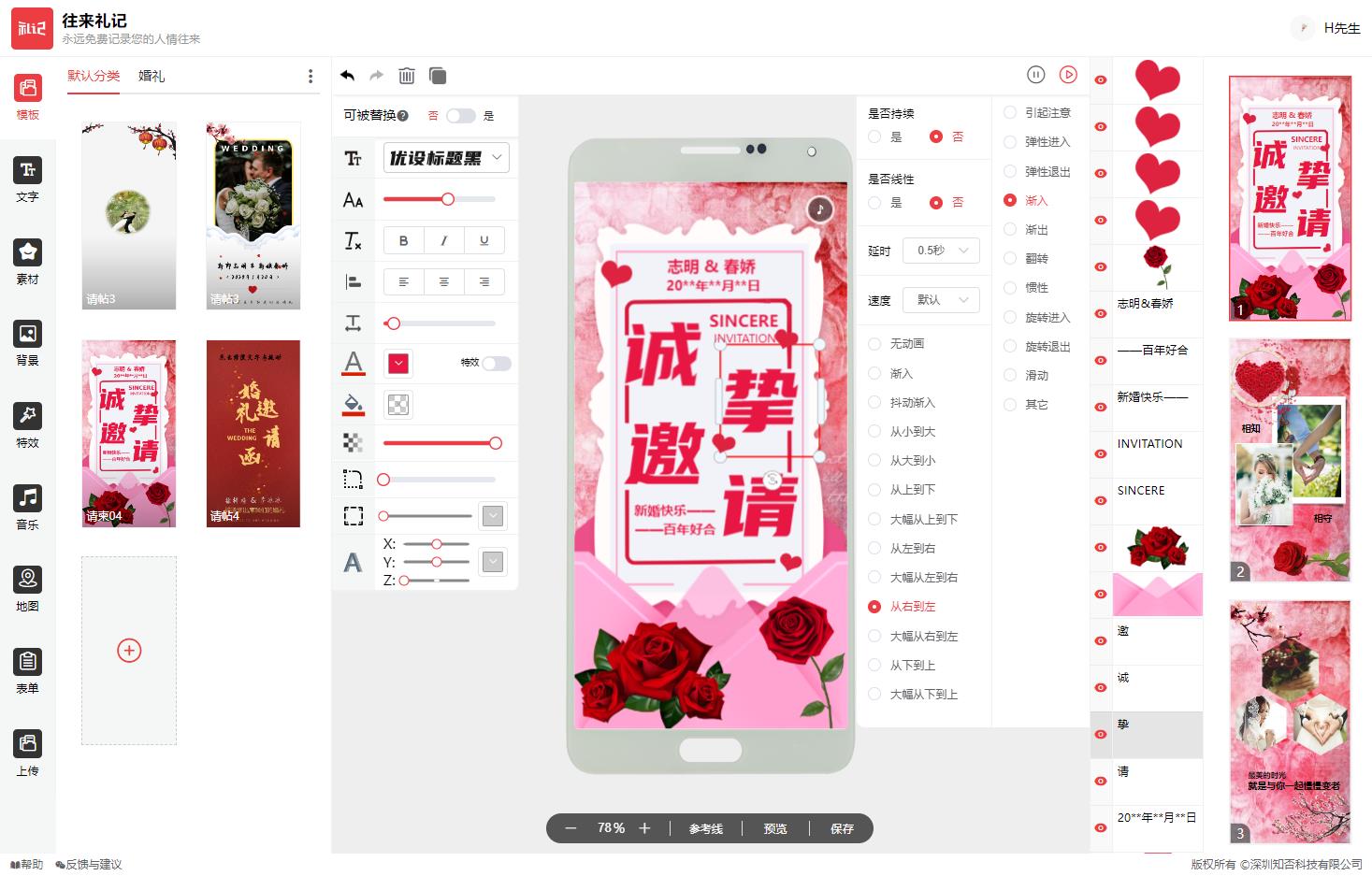
关于请柬邀请函制作
无需任何学习曲线,即可免费、迅速打造您梦寐以求的动态请帖模板!
关于知ing
一款专为大学生打造的考试、考证、阅读、在线交流学习的神器







我们致力于提供更好更优质的服务
知无知,才有知
从“无知”到“知否大学”再到“知ing”,一路走来,非常感谢“知ing”这么多年给大家一直提供这么好的免费服务。可是我即将毕业,好可惜上传资料、学习笔记赚钱的功能上线得太晚,要不然生活就不用愁了。最后祝愿师弟师妹们在“知ing”里有所收获,争做学霸,也祝愿“知ing”在未来提供更好的服务与体验!!!

Student
作为一个老师,刚开始接触这个APP时候我是拒绝的,本以为上这个APP的同学就是冲着抄作业答案而来的,后来我发现绝大部分同学都不是。正如app里那句“做学霸还是学渣你自己选择”的口号一样,没有人愿意成为学渣,比起线下问学霸同学们更愿意在APP里以匿名的方式寻找学霸。

Teacher
为什么这么晚才知道有这么一个APP,自从用了这个APP后才发现身边好多同学都在用,难道同学们都敝帚自珍(O(∩_∩)O哈哈~)?APP里的资料真的很多,感觉大部分教材都能找得到,更重要的是没有也没关系,可以发布悬赏寻求学霸帮助,这简直不要太酷~

Student
超级好用,想要的答案几乎都有,还有一个简单易用的课程表,还可以看小说、查论文...,更重要的是还能赚钱,简直功能不要太齐全哦!爱了爱了!!

Student

如果您有合作意向或者建议,请点击下方给我们留言,我们会定期查看或回复您的留言